Bobo.id - Apakah teman-teman sering menemukan benda-benda yang berbentuk trapesium?
Kita kenali sifat-sifat bangun datar trapesium dan rumus untuk menghitung luas dan kelilingnya, yuk!
Sifat Dasar Trapesium
Trapesium adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk atau garis.
Dari empat rusuk itu, hanya dua rusuk yang saling sejajar. Namun, kedua rusuk yang saling sejajar ini memiliki panjang yang berbeda.
Seperti bangun segi empat lainnya, trapesium juga memiliki empat sudut. Menariknya, dalam sebuah trapesium bisa ada tiga macam sudut sekaligus, yaitu sudut lancip (sudut kurang dari 90°), sudut siku-siku (sudut 90°), dan sudut tumpul (sudut lebih dari 90°).
Baca Juga: Contoh Benda di Rumah yang Bentuknya Tabung, Kerucut, Balok, Kubus, Prisma, dan Bola
Namun, bisa juga hanya dua macam sudut, yaitu tumpul dan lancip. Tiga atau dua macam sudut itu tergantung dengan jenis trapesiumnya.
Ada tiga jenis trapesium, yaitu trapesium sembarang, trapesium sama kaki, dan trapesium siku-siku. Ketiga trapesium ini memiliki sifat yang berbeda-beda.
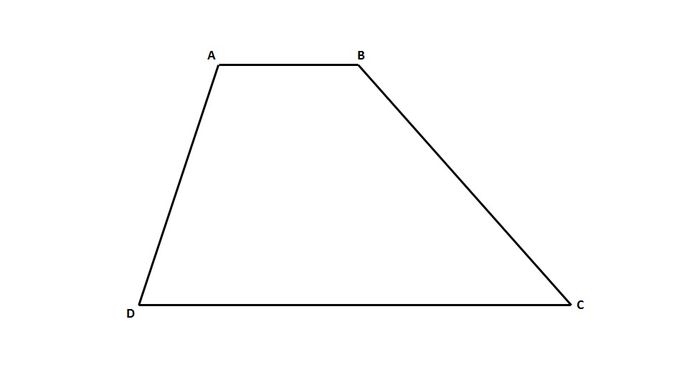
Trapesium Sembarang
Trapesium sembarang adalah trapesium yang ukuran rusuk pada tiap sisinya berbeda-beda. Jadi, pada contoh trapesium ABCD di atas, ukuran AB tidak sama dengan BC, BC tidak sama dengan CD, dan CD tidak sama dengan DA (AB ≠ BC ≠ CD ≠ DA).
Trapesium sembarang tidak punya simetri lipat dan hanya punya satu simetri putar.
Baca Juga: Kerjakan Latihan Soal Matematika tentang Fungsi Kuadrat di Video Ini 
Trapesium Sama Kaki
Trapesium ini memiliki sepasang rusuk yang ukurannya sama panjang. Dua rusuk lainnya sejajar, namun memiliki ukuran yang berbeda. Pada contoh trapesium sama kaki EFGH panjang EH = FG, namun EF ≠ GH.
Selain itu, dua sudut yang bersebelahan pada trapesium sama kaki juga memiliki ukuran yang sama. Jadi, ∠E = ∠F dan ∠G=∠H. Trapesium sama kaki memiliki 1 simetri lipat dan 1 simetri putar.

Trapesium siku-siku adalah trapesium yang memiliki satu atau dua sudut siku-siku.
Jadi, salah satu rusuk dari trapesium ini tegak lurus dengan tinggi trapesium.
Pada contoh trapesium IJKL, sudut L adalah sudut siku-siku dan panjang garis IL sesuai dengan tinggi trapesium.
O iya, karena memiliki sudut siku-siku, teori Phytagoras juga berlaku pada trapesium ini. Trapesium siku-siku tidak memiliki simetri lipat dan hanya memiliki satu simetri putar.
Rumus Keliling dan Luas Trapesium
Meskipun ada 3 jenis trapesium, rumus untuk keliling dan luasnya bisa digunakan pada ketiga trapesium itu.
Untuk mencari keliling trapesium caranya cukup mudah, yaitu menjumlahkan panjang keempat sisi trapesium. Misalnya, pada trapesium ABCD maka cara mencari keliling adalah:
Keliling trapesium = AB + BC + CD + DA
Sedangkan untuk mencari luas trapesium rumusnya adalah:
Luas trapesium = jumlah rusuk sejajar x tinggi : 2
Contoh pada trapesium ABCD di atas, rumusnya menjadi :
Luas trapesium ABCD = (AB+CD) x tinggi : 2
-----
Teman-teman, kalau ingin tahu lebih banyak tentang sains, dongeng fantasi, cerita misteri, dan pengetahuan seru, langsung saja berlangganan majalah Bobo dan Mombi SD. Tinggal klik di https://www.gridstore.id
Atau teman-teman bisa baca versi elektronik (e-Magz) yang dapat diakses secara online di ebooks.gramedia.com
| Penulis | : | Eva Jessica |
| Editor | : | Avisena Ashari |
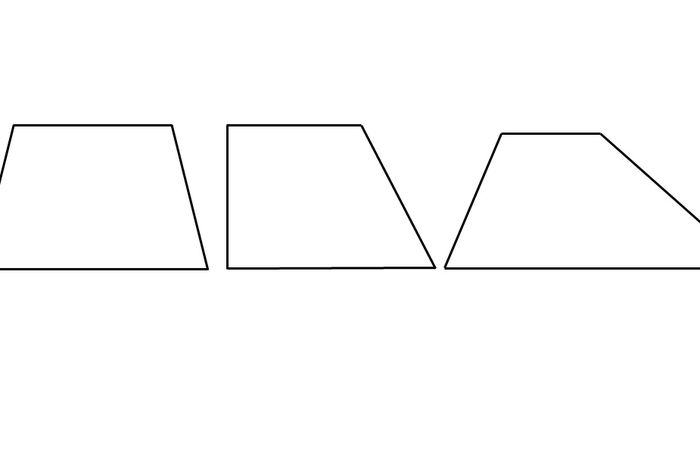
KOMENTAR